Unveiling the Mathematical Wonders of Hot Air Balloons: A Journey into Science and Engineering

The Allure of Hot Air Balloons

Hot air balloons, with their captivating silhouettes and vibrant hues, have captivated human imagination for centuries. These majestic aerial wonders are not merely whimsical creations but intricate vessels governed by the principles of mathematics and engineering. This article delves into the fascinating intersection of these disciplines, uncovering the mathematical marvels that make hot air ballooning an enchanting pursuit.
4.3 out of 5
| Language | : | English |
| File size | : | 11335 KB |
| Screen Reader | : | Supported |
| Print length | : | 32 pages |
| Hardcover | : | 85 pages |
| Item Weight | : | 6.4 ounces |
| Dimensions | : | 6 x 0.39 x 9 inches |
The Science of Buoyancy: Lighter than Air
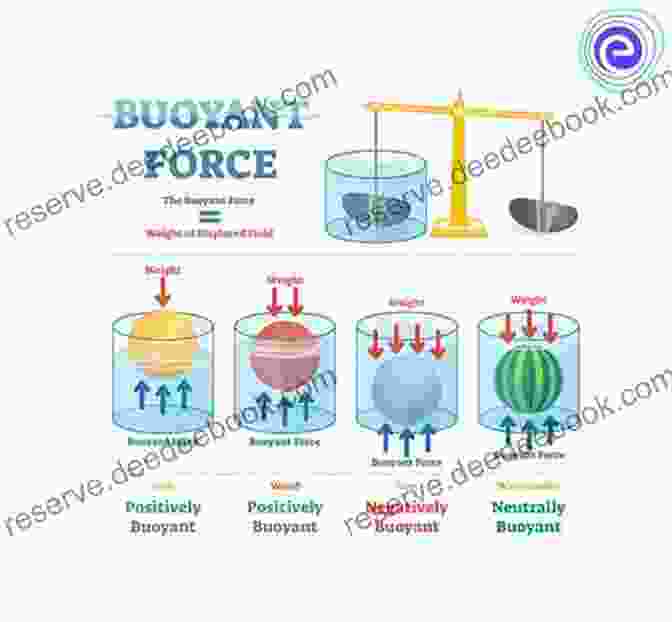
At the heart of hot air ballooning lies the concept of buoyancy, a fundamental force that allows objects to float. Hot air balloons rely on the principle of Archimedes, which states that an object submerged in a fluid (in this case, air) experiences an upward force equal to the weight of the fluid displaced by the object. By heating the air inside the balloon, we effectively reduce its density, causing it to become less dense than the surrounding air. This difference in density creates an upward force, the buoyant force, which counteracts the weight of the balloon and its occupants.
Mathematically, the buoyant force (Fb) is given by the following equation:
Fb = ρair * g * V
where:
- ρair represents the density of the surrounding air
- g is the acceleration due to gravity
- V is the volume of air displaced by the balloon
By increasing the volume of the balloon or decreasing the density of the air inside, we can enhance the buoyant force, allowing the balloon to ascend.
Harnessing Aerodynamics

Once airborne, hot air balloons must contend with the forces of aerodynamics. The balloon's shape, combined with the movement of air around it, dictates its stability and maneuverability. The iconic spherical shape of hot air balloons provides optimal volume while minimizing drag, reducing resistance to airflow. The burner, located at the base of the balloon, generates heated air, which rises and exits through the top of the balloon, creating a Venturi effect that further enhances lift.
Understanding the principles of aerodynamics allows balloonists to control the direction and altitude of their crafts. By adjusting the burner's output and manipulating the balloon's orientation, they can navigate air currents, ascend to greater heights, or descend smoothly when desired.
Geometry: Shaping and Sizing

Geometry plays a pivotal role in the design and construction of hot air balloons. The balloon's shape is not merely aesthetic but also serves to optimize lift and stability. The spherical shape, as mentioned earlier, minimizes drag, while the conical shape of the balloon's top helps channel rising air, further enhancing buoyancy. Additionally, the size of the balloon must be carefully calculated to ensure sufficient lift for the intended payload and meteorological conditions.
The mathematics of geometry provides the framework for designing balloons that are both efficient and aesthetically pleasing. By meticulously crafting the balloon's shape and dimensions, engineers can ensure optimal performance and safety during flight.
The Art of Navigation

Navigating a hot air balloon presents a unique set of challenges. Unlike aircraft with engines and rudders, balloons rely on the wind and the skill of the pilot to reach their destination. Balloonists utilize a combination of mathematical calculations and observation to determine their position, track their progress, and plan their flight path.
Trigonometry and geometry come into play when calculating distances and angles. By measuring the balloon's elevation, the pilot can estimate the distance traveled and determine the direction of their flight. Wind speed and direction are also critical factors to consider, and balloonists use vector analysis to account for these variables and adjust their course accordingly.

Hot air ballooning is a testament to the power of mathematics and engineering. By understanding the principles of buoyancy, aerodynamics, geometry, and navigation, balloonists can soar through the skies, marveling at the breathtaking scenery while experiencing the thrill of flight. The mathematical wonders that govern these majestic vessels make hot air ballooning not only an awe-inspiring spectacle but also a fascinating exploration into the realm of science and engineering.
So, the next time you witness the enchanting sight of a hot air balloon drifting effortlessly in the heavens, take a moment to appreciate the intricate mathematics and engineering that make this aerial marvel possible.
4.3 out of 5
| Language | : | English |
| File size | : | 11335 KB |
| Screen Reader | : | Supported |
| Print length | : | 32 pages |
| Hardcover | : | 85 pages |
| Item Weight | : | 6.4 ounces |
| Dimensions | : | 6 x 0.39 x 9 inches |
Do you want to contribute by writing guest posts on this blog?
Please contact us and send us a resume of previous articles that you have written.
 Novel
Novel Page
Page Genre
Genre Reader
Reader Newspaper
Newspaper Paragraph
Paragraph Sentence
Sentence Bookmark
Bookmark Shelf
Shelf Glossary
Glossary Preface
Preface Annotation
Annotation Footnote
Footnote Scroll
Scroll Bestseller
Bestseller Classics
Classics Library card
Library card Autobiography
Autobiography Memoir
Memoir Encyclopedia
Encyclopedia Dictionary
Dictionary Thesaurus
Thesaurus Narrator
Narrator Character
Character Librarian
Librarian Catalog
Catalog Borrowing
Borrowing Study
Study Scholarly
Scholarly Lending
Lending Reserve
Reserve Academic
Academic Journals
Journals Rare Books
Rare Books Interlibrary
Interlibrary Study Group
Study Group Awards
Awards Reading List
Reading List Theory
Theory Textbooks
Textbooks Barry Cannon
Barry Cannon Zoe Blake
Zoe Blake David Walters
David Walters Jay Arthur
Jay Arthur Rayna Rose Exelbierd
Rayna Rose Exelbierd Mauro Canali
Mauro Canali Melanie Mason
Melanie Mason Laurie Mcelroy
Laurie Mcelroy Karel Capek
Karel Capek Shawna Stewart
Shawna Stewart Henry Kissinger
Henry Kissinger Ali Lowe
Ali Lowe Patrizio Kroyani
Patrizio Kroyani Greta Van Susteren
Greta Van Susteren Jeffrey Ross
Jeffrey Ross Julie Kagawa
Julie Kagawa Joseph Kerman
Joseph Kerman Caroline L Walker
Caroline L Walker Ana Andjelic
Ana Andjelic Walter Trobisch
Walter Trobisch
Light bulbAdvertise smarter! Our strategic ad space ensures maximum exposure. Reserve your spot today!

 Ervin BellCome With Me to New York: A Journey Through the Heart of the City That Never...
Ervin BellCome With Me to New York: A Journey Through the Heart of the City That Never... Fernando PessoaFollow ·16.9k
Fernando PessoaFollow ·16.9k Jonathan HayesFollow ·18.9k
Jonathan HayesFollow ·18.9k Martin CoxFollow ·10.9k
Martin CoxFollow ·10.9k John KeatsFollow ·16.4k
John KeatsFollow ·16.4k Neal WardFollow ·15.5k
Neal WardFollow ·15.5k Gabriel HayesFollow ·3.8k
Gabriel HayesFollow ·3.8k Pete BlairFollow ·11.6k
Pete BlairFollow ·11.6k Tyler NelsonFollow ·13.4k
Tyler NelsonFollow ·13.4k

 Barry Bryant
Barry BryantAn Immersive Exploration into the World of Big Note Sheet...
: Embarking on a Musical Odyssey The pursuit...

 Corey Green
Corey GreenPolitics And The Street In Democratic Athens
The streets of democratic Athens...

 Ian McEwan
Ian McEwanThe Extraordinary Life of Fifth Officer Harold Lowe: From...
Harold Godfrey Lowe (21...

 Zachary Cox
Zachary CoxDiscover Jay Town: A Place Where High Fives and Community...
Nestled amidst rolling hills and...

 Oscar Wilde
Oscar WildeThe Kishangarh School Of Indian Art: True Sense And...
Amidst the diverse tapestry of Indian art,...

 Michael Simmons
Michael SimmonsCuban Flute Style Interpretation and Improvisation: A...
The Cuban flute style is a...
4.3 out of 5
| Language | : | English |
| File size | : | 11335 KB |
| Screen Reader | : | Supported |
| Print length | : | 32 pages |
| Hardcover | : | 85 pages |
| Item Weight | : | 6.4 ounces |
| Dimensions | : | 6 x 0.39 x 9 inches |










